Semaphores in Uppaal
Version 4.0 of Uppaal includes C-like syntax for defining functions.
This new syntax makes it possible to define very simple and elegant models of semaphores.
This webpage briefly describes the semaphore models and how they can
be used to solve some nontrivial concurrency problems taken from William Stallings,
Operating Systems: Internals and Design Principles, seventh edition,
Pearson Education Limited 2012.
For more information, see also our paper on this subject.
Since Uppaal does not include the concept of a blocked process,
we take a slightly more abstract view in modeling semaphores:
when a process does a Wait on a semaphore it may only proceed
after subsequent receipt of a Go message.
If the semaphore has a positive value it will issue such a message
immediately.
Otherwise, the process id will be entered in a queue, and the
Go message will be sent later when the process
id is removed from the queue as a result of a Signal.
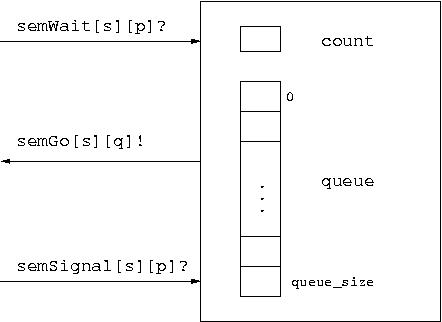
Technically, a semaphore s is modeled as an automaton that
interacts with its environment through three sorts of synchronization
actions: semWait[s][p]?, semSignal[s][p]? and
semGo[s][p]!, where p is some process id in the
interval [0,N-1].
The semaphore template has three parameters of type integer:
(1) id, the unique identifier of the semaphore,
(2) init_val, the initial value of the semaphore, and
(3) queue_size, the maximal number of processes in the waiting queue.
Since Uppaal does not support dynamically growing data structures,
we need to fix an upper bound on the size of the queue.
In our model, the queue is implemented as an array of queue_size.
The semaphore also has an integer state variable count, which records
the current value of the semaphore.
The model is schematically depected below.
The Uppaal files for the model are available at
In this model the semaphore is used to achieve mutual exclusion for four processes.
Some comments on the model:
-
Since currently in Uppaal it is not possible to initialize a parametrized
array, we need a special transition to do this.
This imperfection of Uppaal actually has a positive consequence:
due to the extra transition the automaton looks like a honeybee!
By making the initial location "committed" we ensure that the
initialization takes place before any other activity in the
system. (In Uppaal, outgoing transitions of a committed location
have priority and must be carried out immediately.)
-
In five transitions we use a select field p int[0,N-1].
This simply means that we have instances of these transitions for
each p in the interval [0,N-1], that is, for each process.
-
In Dijkstra's orgininal definition, count is not further decreased
when it is 0 and a semWait occurs.
Stalling does decrease the count in this case.
It does not make any difference for either the observable behavior
of the semaphore automaton or in terms of the number of reachable states.
I slightly prefer Dijkstra's definition but decided to follow Stallings here,
since I am using the examples from his book.
An advantage of Stallings' definition is that when count is negative
its value tells you how many processes are waiting. With Dijkstra's definition
you don't have that information readily available.
-
In case a semWait occurs when count is positive,
or a semSignal occurs when count is negative,
the automaton perfoms a semGo transition.
I have made the start location of this transition committed, to
express that the semGo is generated in a single atomic
transaction with the preceding semWait or semSignal.
An auxiliary variable q is required to store the id of the
process to which the semGo signal is sent.
-
The definitions of the various operations on the queue (enQueue(p),
deQueue(), etc) are straightforward.
My objective has been to optimize on the use of memory rather than on
computation time. So, for instance, I did not introduce pointer variables to
store the first empty position in the array but just compute this position with
a simple while loop in the body of the enQueue function.
In model checking, memory usage is typically the bottleneck and so it is
important to minimize the number of state variables.
-
Each semWait(s) operation by a process p that is using semaphore s
translates to two consecutive transitions labeled with synchronization actions
semWait[s][p]! and semGo[s][p]?, respectively.
Each semSignal(s) operation by p is encoded by a transition
with synchronization action semSignal[s][p]!.
-
Correctness properties that can be verified using Uppaal include
(a) mutual exclusion, (b) absence of deadlock, (b) no queue overflow.
The Uppaal model for the binary semaphore is a small and obvious variation
of the general semaphore model. It is available at
Tackling Concurrency Problems
Now we have models of semaphores, we can start playing with them!
The Barrier Problem
Here is an alternative solution to the barrier synchronization problem discussed by Downey
in section 3.5 of his book:
The Producer/Consumer Problem
Here is a model of the incorrect solution to the Infinite-Buffer Producer/Consumer Problem
using Binary Semaphores, discussed by Stallings on pages 239-242:
The model is obtained in a straightforward manner from the code presented
by Stallings in Fig 5.9.
As Stallings point out, the problem with this solution is that variable
n may become negative, that is, the consumer may consume an
item from the buffer that does not exist.
By posing the query E<> n<0 to the verifier ("there exists a path
to a state in which n<0"), Uppaal produces a counterexample
almost instantaneously.
Essentially (modulo permutation of independent transitions), this is the same
counterexample as the one presented by Stallings in Table 5.4.
The ability of the Uppaal simulator to replay the counterexample
greatly helps in understanding what goes wrong.
Note that Uppaal is not able to explore the full (inifinite) state space of this model.
I also looked at the solution to the Bounded-Buffer Producer/Consumer Problem Using Semaphores
presented by Stallings in Figure 5.13:
Stallings claims correctness of this solution, but does not prove it.
Even for large values of sizeofbuffer like 10.000,
Uppaal can prove mutual exclusion and absence of deadlock
automatically within a few seconds
After introducing an auxiliary variable buffer that is
incremented by function produce() and decremented
by function consume(), Uppaal can prove the invariant
property buffer >=0 and buffer <= sizeofbuffer, that is
the consumer never consumes an item that does not exist, and
there is no buffer overflow.
The above solution to the Bounded-Buffer Producer/Consumer Problem is
also presented by Tanenbaum and Woodhul in their textbook on Operating Systems (Second Edition).
The authors observe that when the order of the Wait operations in the Producer code
is reversed there is a deadlock.
This observation can easily be verified using Uppaal:
Dining Philosophers
In Section 6.6, Stalling discusses the Dining Philosophers problem.
Of course, it is trivial to encode "solutions" to the Dining Philosophers problem
in Uppaal, find deadlocks, etc
Barbershop
Two students, Albert Gerritsen and Allan van Hulst, encoded the unfair barbershop
described in Appendix A.3 of Stallings book. Using the symmetry reduction feature
of Uppaal they analyzed this model for, e.g., 2 barbers and 8 customers.
Room Party Problem
An wonderful source of concurrency problems is Downey's The Little Book of Semaphores.
Marc Schoolderman pointed out that Downey's solution to the so-called "room party" problem as it was described in an earlier edition is incorrect.
Lounge

